 mavoe Informatik
mavoe Informatik Martin privat
Martin privatÖffentliche Nachricht
Impressum / Datenschutz
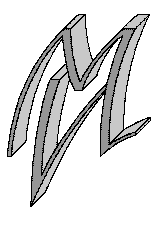
| k | = | Klartext |
| c | = | Chiffretext |
| V | = | Verschlüsselungs-Funktion |
| E | = | Entschlüsselungs-Funktion |
| s | = | symmetrischer Schlüssel |
| o | = | öffentlicher Schlüssel |
| g | = | geheimer Schlüssel |
| u | = | Unterschrift
|
| c | = | V(s,k) |
| k | = | E(s,c) |
| k | = | E(s,V(s,k))
|
| k | = | Element aus der Menge aller Wörter ueber demAlphabet (a, b, ... , z) |
| s | = | Element aus (0, 1, 2, ... , 25) |
| V(s,k) | = | Abbildung jedes Buchstaben eines Wortes auf den Buchstaben der s Stellen später im Alphabeth steht; dabei wird nach dem letzen Buchstaben wieder beim ersten angefangen (Addition modulo 26) |
| E(s,c) | = | V(26-s,c) |
| V(1,abc) | = | bcd |
| V(5,auto) | = | fzyt |
| V(0,duden) | = | duden |
| V(25,computer) | = | bnlotsdq |
| V(1,bnlotsdq) | = | computer |
| c | = | V(o,k) |
| k | = | E(g,c) |
| k | = | E(g,V(o,k)) |
aber auch (!):
| u | = | E(g,k) |
| k | = | V(o,u) |
| k | = | V(o,E(g,k) |
Das Verfahren funktioniert dann, wenn weder aus Kenntniss es öffentlichen Schlüssels der geheime Schlüssel berechnet werden kann, noch aus einem Chiffretext (oder einer Unterschrift) der geheime Schlüssel berechnet werden kann.
| o´ | = | öffentlicher Schlüssel von Otto |
| g´ | = | geheimer Schlüssel von Otto |
| o" | = | öffenlicher Schlüssel von Lisa |
| g" | = | geheimer Schlüssel von Lisa |
| u | = | E(g´,k) |
| c | = | V(o", u) |
| Otto schickt Lisa c ueber einen unsicheren Kanal | ||
| u | = | E(g",c) |
| k | = | V(o´,u) |
Solang Otto seinen geheimen Schlüssel nicht verliert, kann Lisa sicher sein, daß die Nachricht k von Otto kommt.
Für unterschriebene, öffentliche Nachrichten wird mit nicht umkehrbaren Hash-Algorithmen (z.B. MD5) eine kurze Quersumme aus dem Text berechnet und diese mit dem geheimen Schlüssel des Autors verschlüsselt an die Nachricht angefügt.
... RSA ist Bestandteil vieler offizieller Standards (z.B. PEM (Internet Privacy Enhanced Mail) oder SWIFT (Society for Worldwide Interbank Financial Telecommunication)) ...
... RSA wird ... haeufig in Chip-Karten, die zur Benutzerauthentifikation eingesetzt werden, genutzt ...
Beide Zitate stammen von Dr. Claudia Eckert
| k in ASCII | = | R | S | A | w | o | r | k | s | ! | |
| k in dez. ASCII | = | 82 | 83 | 65 | 32 | 119 | 111 | 114 | 107 | 115 | 33 |
| k in 2er Blöcken | = | 21075 | 16672 | 30575 | 29291 | 29473 | |||||
| c in 2er Blöcken | = | 48467 | 14579 | 26195 | 58004 | 30141 | |||||
2er Blöcke weil 2**16 = 65536 < n - 1 (siehe unten)
Mit größerem n können die Blöcke entsprechend größer
sein. In der Praxis hat n mindestens 100 Dezimalstellen.
Ver- und Entschlüsselung
Dann ist:
| V(k) | = | k ** e mod n | mit k < n |
| E(c) | = | c ** d mod n | mit c < n |
e und n sind der öffentliche Schlüssel
d (und n) sind der geheime Schlüssel
Außer auf eine gleichmäßige Verteilung der generierten Zufallszahlen kommt es darauf an, daß die Reihnfolge der generierten Zufallszahlen nicht vorhersagbar ist. Das kann z.B. durch einen echt zufälligen Startwert der Zufallszahlen-Berechnung erreicht werden.
Folgendes Programmstück wählt eine z.B. 100-stellige Primzahl aus:
repeat
Primzahlsatz:
Die Wahrscheinlichkeit in (1, ... p) bei zufälliger Auswahl eine Primzahl zu finden
ist ca. = (p / ln(p)) / p = 1 / ln(p)
Daher benötigt man im Durchschnitt ln(p) viele Versuche,
bis man eine Primzahl gefunden hat.
ln(10 ** 100) ca. = 230
Wenn dieser Algorithmus "nein" ausgibt, dann ist die zu prüfende Zahl keine Primzahl. Wenn dieser Algorithmus "ja" ausgibt, dann stimmt dieses Ergebnis mit einer Wahrscheinlichkeit von 0,5 (stochastischer Algorithmus).
Bei m-maligem Aufruf verringert sich die Fehlerwahrscheinlichkeit auf 0,5 ** m , sofern auf unterschiedliche Werte für a (s.u.) geachtet wird. Zum Vergleich einige persönliche Wahrscheinlichkeiten:
| Blitzschlag pro Jahr | = | 10 ** -7 | > 0,5 ** 24 |
| Lottogewinn | = | 7 * 10 ** -8 | > 0,5 ** 24 |
| Meteortreffer pro Jahr | = | 10 ** -12 | > 0,5 ** 40 |
procedur primtest(p)
/* Die zu prüfende Zahl muß ungerade sein. */
var a, eps, delta, p: integer
a = randomize (1, p - 1)
if ggT(a, p) = 1 then
function jabobi(a, p: integer): integer
if a = 1
then jacobi := 1
else
function ggT(a, b: integer): integer
repeat
function m_invers(d, phi: integer): integer
e = 0
ee = 1
repeat
function hochmod(k, e, n: integer): integer
b = Binaer(e)
h = 1
do i = Length(b) - 1 to 0 by -1
| k | = | 21075 (siehe oben) | ||
| p | = | 251 (Primzahl) | ||
| q | = | 269 (Primzahl) | ||
| n | = | p * q | = | 67519 |
| phi(n) | = | (p - 1) * (q - 1) | = | 67000 |
Waehle d mit d < n und ggT(phi(n),d) = 1
d = 27917
ggT (Algorithmus siehe oben)
| a = d | b = phi(n) | r |
| 27917 | 67000 | 27917 |
| 67000 | 27917 | 11166 |
| 27917 | 11166 | 5585 |
| 11166 | 5585 | 5581 |
| 5585 | 5581 | 4 |
| 5581 | 4 | 1 |
| 4 | 1 | 0 |
de = 1 mod phi(n) =>
e = 50253
Multiplikative Inverse (Algorithmus siehe oben)
| e | ee | d | Y | q | r |
| 0 | 1 | 27917 | 67000 | 0 | 27917 |
| 1 | 0 | 67000 | 27917 | 2 | 11166 |
| -2 | 1 | 27917 | 11166 | 2 | 5585 |
| 5 | -2 | 11166 | 5585 | 1 | 5581 |
| -7 | 5 | 5585 | 5581 | 1 | 4 |
| 12 | -7 | 5581 | 4 | 1395 | 1 |
| -16747 | 12 | 4 | 1 | 4 | 0 |
k ** e mod n berechnen (Algorithmus siehe oben)
21075 ** 50253 mod 67519
50253 = 1100010001001101 = b
| i | h | Beispiel für einen Rechenschritt | |
|---|---|---|---|
| 1 | 15 | 1 21075 |
21075**2/67519=6578,231682933693 0,231682933693*67519=15643,000000018 |
| 1 | 14 | 15643 48467 | |
| 0 | 13 | 64079 | |
| 0 | 12 | 17775 | |
| ... | |||
| 1 | 2 | 12634 34133 | |
| 0 | 1 | 21344 | |
| 1 | 0 | 15643 48467 | |
c ** d mod n berechnen (Algorithmus siehe oben)
48467 ** 27917 mod 67519
27917 = 110110100001101
| i | h | |
|---|---|---|
| 1 | 14 | 1 48467 |
| 1 | 13 | 64079 45450 |
| 0 | 12 | 26214 |
| 1 | 11 | 32933 14551 |
| ... | ||
| 1 | 2 | 7652 55136 |
| 0 | 1 | 3040 |
| 1 | 0 | 59016 21075 |
In der Literatur wird diskutiert, ob p , q und d so gewaehlt werden koennen, dass der RSA-Algorithmus besonders sicher ist.
Prof. Dr. Uwe Schoening, S. 179: Wir haben also gesehen, daß es effiziente Primzahlentests gibt (...). Wenn der Primzahltest aber "keine Primzahl" ausgibt, so handelt es sich um eine Zahl, die sich in nicht-triviale Faktoren zerlegen läßt. Wir sind aber weit davon entfernt, solche Faktoren in effizienter Weise zu erhalten. Nehmen wir an, n ist das Produkt zweier 100-stelliger Primzahlen p und q . Die Aufgabe, aus einer solchen gegebenen Zahl n = p q die Faktoren p und q rückzugewinnen, ist auch mit heutigen Computern eine "praktisch unlösbare" Aufgabe. Eine solche Berechnung würde Jahrtausende dauern.
Dr. Claudia Eckert, S. 124: Je größer der Modul gewählt wird, desto schwieriger ist es, den Schlüssel zu brechen ... Eine gute Analyse der Sicherheit eines Moduls festgelegter Länge ist in "R.L. Rivest: 'Response to NIST's proposal', Communication of the ACM, 35(7):41-47, July 1992" zu finden. Aus den Analysen ist abzuleiten, daß ein 512-bit langer Modul in der Zukunft mit einem finanziellen Aufwand unter $ 8,2 Millionen gebrochen werden kann, so daß längere Modulen, z.B. 768-bit in der Zukunft empfohlen werden.
Klartextblock (64 Bit)
Runde 1
Teilblock Teilblock Teilblock Teilblock
(16 Bit) (16 Bit) (16 Bit) (16 Bit)
| | | |
V V V V
S1,1->MULT S1,2->ADD S1,3->ADD S1,4->MULT
| | | |
+------->XOR <--------------------------+ |
| | | | |
| | +--------------------------->XOR <-------+
| | | | | |
| V | | V |
| S1,5->MULT----------------------------------->ADD |
| | | | | |
| V | | V |
| ADD <----------------+------------------MULT<-S1,6 |
| | | | | |
V | | | V |
XOR <--------------------------+------->XOR |
| | | | |
| +-------------------+ | |
| | | | |
| V | | V
| XOR <------+---------------------------->XOR
| | | |
| +---------+ | |
| | | |
| +-------------------+ |
| | | |
| | +---------+ |
| | | |
V V V V
Runde 2-8 mit den Schluesseln 2 bis 8
| | | |
| +---------+ | |
| | | |
| +-------------------+ |
| | | |
| | +---------+ |
| | | |
V V V V
S9,1->MULT S9,2->ADD S9,3->ADD S9,4->MULT
| | | |
V V V V
Teilblock Teilblock Teilblock Teilblock
(16 Bit) (16 Bit) (16 Bit) (16 Bit)
Chiffretextblock (64 Bit)
XOR = Bitweise Addition zweier Zahlen ohne Uebertrag
ADD = Addition zweier Zahlen ohne Beruecksichtigung des
Uebertrags ueber 2**16 hinaus
MULT = Multiplikation zweiter Zahlen und Bildung des Restes
nach Division durch 2**16+1. Hierbei werden 0 und
2**16 besonders behandelt: Vor Beginn der
Multiplikation wird 0 durch 2*16 ersetzt, das
Ergebnis 2**16 wiederum wird als 0 interpretiert.
Daraus folgt: 0 "mal" 0 = 1.
128-Bit-Schluessel in 8 Bloecke a 16 Bit aufteilen
------------------------------------------------
| | | | | 1 1 | 1
1 | 2 3 | 4 | | 9 | 0 1 | 2
1234567890123456|7890123456789012|3456789012345678| ... |1234567890123456|7890123456789012|3456789012345678
| | | | | |
S1,1 | S1,2 | S1,3 | | S1,6 | S2,1 | S2,2
25 Bit nach links rotieren
| | | | 1 1 | |
3 4 | 5 | 6 7 | | 1 2 | |1 2
6789012345678901|2345678901234567|8901234567890123| ... |6789012345678901|2345678123456789|0123456789012345
| | | | | |
S2,3 | S2,4 | S2,5 | | S3,2 | S3,3 | S3,4
usw. bis
| | | | 1 | 1 |
3 | 4 5 | 6 | | 1 | 2 | 1 2
2345678901234567|8901234567890123|4567890123456789| ... |2345678901234567|8901234567812345|6789012345678901
| | | | | |
S9,1 | S9,2 | S9,3 | | | |
Entschluesseln nach IDEA
-----------------------
Teilschluessel
1 2 3 4 5 6
R 1 1/S9,1 -S9,2 -S9,3 1/S9,4 1/S8,5 -S8,6
u 2 1/S8,1 -S8,2 -S8,3 1/S8,4 1/S7,5 -S7,6
n ...
d 8 1/S2,1 -S2,2 -S2,3 1/S2,4 1/S1,5 -S1,6
e Ende 1/S1,1 -S1,2 -S1,3 1/S1,4
So far, IDEA has resisted attack much better than other ciphers such as FEAL, REDOC-II, LOKI, Snefru and Khafre. And recent evidence suggests that IDEA is more resistant than the DES to Biham & Shamir's highly successful differential cryptanalysis attack. Biham and Shamir have been examining the IDEA cipher for weaknesses, without success. Academic cryptanalyst groups in Belgium, England, and Germany are also attempting to attack it, as well as the military services from several European countries. As this new cipher continues to attract attack efforts from the most formidable quarters of the cryptanalytic world, confidence in IDEA is growing with the passage of time.
People who work in factoring research say that the workload to exhaust all the possible 128-bit keys in the IDEA cipher would roughly equal the factoring workload to crack a 3100- bit RSA key, which is quite a bit bigger than the 1024-bit RSA key size that most people use for high security applications. Given this range of key sizes, and assuming there are no hidden weaknesses in the conventional cipher, the weak link in this hybrid approach is in the public key algorithm, not the conventional cipher.
Überlegen Sie sich bitte in Zweiergruppen ein RSA-Schlüsselpaar und verschlüsseln Sie bitte anschließend eine passende Zahl damit - z.B. einen Teil Ihres Geburtsdatums oder Ihrer Postleitzahl. Tauschen Sie bitte die verschlüsselte Zahl und ihren öffentlichen Schlüssel mit einer anderen Arbeitsgruppe aus und entschlüsseln Sie bitte anschließend deren RSA verschlüsselte Zahl mit deren öffentlichem RSA-Schlüssel.
Benutzen Sie bitte für diese Übung, je nach Kenntnisstand, Papier und Bleistift, einen Taschenrechner, eine Tabellenkalkulation oder eine Programmiersprache.